Shooting stars and doji’s abound.
 As I looked through the charts last night, I saw a lot of shooting stars and Doji’s at highs which are considered bearish. I also saw a lot of indecisive doji’s at highs and in consolidations. Both of these conditions would warrant significant caution. However, there was also a lot of very bullish patterns and some fantastic looking charts. What’s a guy to do? Yesterday was a very emotional day for the market due to the congressional hearings. There were several full reversal whipsaws during the day making charts very convoluted. As of now I’m staying bullish on the overall market and may even consider adding some risk ahead of the weekend, but I will give the market a good 30 minutes to an hour to settle in before making any decisions.
As I looked through the charts last night, I saw a lot of shooting stars and Doji’s at highs which are considered bearish. I also saw a lot of indecisive doji’s at highs and in consolidations. Both of these conditions would warrant significant caution. However, there was also a lot of very bullish patterns and some fantastic looking charts. What’s a guy to do? Yesterday was a very emotional day for the market due to the congressional hearings. There were several full reversal whipsaws during the day making charts very convoluted. As of now I’m staying bullish on the overall market and may even consider adding some risk ahead of the weekend, but I will give the market a good 30 minutes to an hour to settle in before making any decisions.
On the Calendar
A very light Friday on the Economic Calendar with only a couple reports with little to no significance. On the Earnings Calendar, it’s much the same with only eight companies reporting. None of which should be market moving. Truly the quiet before the storm, because next week we have one of the fullest calendars of market moving reports I’ve seen in a long time. Of course, the biggest is the FOMC decision on interest rates.
Our news filled day yesterday turned out to be a non-event the U.K. elections could create some turmoil abroad and is worth noting. Long story short, the Prime Minister lost so may key seats it would normally force her resignation. However, she is refusing to resign and will now seek the approval of the Queen to form a government. Let the drama begin!
Action Plan
As you know Friday is normally my day to take some profits and a day I usually restrict myself from adding new positions. However, with the decks, somewhat cleared for the President to proceed with his plans; And the house passing the bill that removes much of the Dodd-Frank debacle I’m thinking of adding risk. The big banks began a rally yesterday, and I would expect that to continue today. Futures have the chances of that the FOMC will raise interest rates next week above 95% which should help the banks even more. Hince, I will be looking for an entry in the financial sector. Stay tuned.
[button_2 color=”green” align=”center” href=”https://youtu.be/LUbGf3J2QfI”]Morning Market Prep Video[/button_2]
Trade Wisely,
Doug
Is there a storm on the horizon or just a lot of hot air?
 Today’s market is filled with news-driven events most of them political in nature. Could there be a storm on the horizon or will it be nothing more than a lot of hot air blowing around? Who knows but one thing for sure is that it is likely to be great fodder for Saturday Night Live skits! I would recommend caution with the futures pointing to a gap up open ahead of all the events about to unfold this morning. Anything is possible, and I think it would be wise to plan for whippy price action today. As the drama is acted out on both sides of the political isle swift price moves are possible. Although I will looking for new trades, I have no desire to compete with a three ring circus. As a result, so I will be waiting for price action to settle and show me the way.
Today’s market is filled with news-driven events most of them political in nature. Could there be a storm on the horizon or will it be nothing more than a lot of hot air blowing around? Who knows but one thing for sure is that it is likely to be great fodder for Saturday Night Live skits! I would recommend caution with the futures pointing to a gap up open ahead of all the events about to unfold this morning. Anything is possible, and I think it would be wise to plan for whippy price action today. As the drama is acted out on both sides of the political isle swift price moves are possible. Although I will looking for new trades, I have no desire to compete with a three ring circus. As a result, so I will be waiting for price action to settle and show me the way.
On the Calendar
Today we have a lot for the market to chew on, but most of it is not on the Economic Calendar. First up we have the weekly Jobless Claims at 8:30 AM Eastern. Claims continue to be unusually low pointing to a strong labor market. The positive trend is expected to continue with the number released this morning. In fact, it would likely have to come in as a huge surprise to move the market.
On the Earnings Calendar, there are 36 companies expected to report today. Marke sure to check current holdings and new purchases for potential earnings reports.
The big events will be in the news today. First off we have ECB decision this morning with a speech following by Draghi. Obviously, this can move the market if there is something unexpected revealed. Later today at 10 AM the circus act in Congress will begin the testimony from Jame Comey. The market saw a slight rally yesterday when details of his interactions with the President were released. It would appear that there is no smoking gun despite all the rhetoric. Of course, if something groundbreaking said during the testimony the market could react wildly so plan accordingly. There is also the possibility of market turmoil with the parliamentary elections in the U.K. and their impacts on Brexit. A wild and wooly day to be certain.
Action Plan
With so much potential market moving news this morning I want to be very cautious this morning. Currently, the futures are pointing to a gap up open setting the stage for a whipsaw price action ahead of all the news. If something unexpected happens to be revealed in the Comey congressional dog and pony show swift price moves are likely to occur. Anything is possible today so have a well thought out plan for current holdings as well as new positions you are considering. I will be looking for new trades, but I will move slowly as these events unfold.
Another issue to be mindful of is the unusual price action of bonds moving higher with the market. Normally bonds would decline as the market rises, but right now bonds have been gaining ground right alongside the overall market. I’m not suggesting this is signaling impending doom, in fact, I don’t know what to make of it, but I do think it requires our attention. Perhaps it’s nothing, but it is odd and may be providing clues to growing market fears.
[button_2 color=”green” align=”center” href=”https://youtu.be/4J2Hc2dUwx8″]Morning Market Prep Video[/button_2]
Trade Wisely,
Doug
Price Above T-Line For The Twelfth Day
(SPY) Yesterday the SPY closed plus .19% with a Doji. And the Bulls have kept the price above the T-Line for the twelveth day. We currently have a 3 bar pullback; this could be a setup for a J-Hook continuation pattern. Two of the four pieces are in place. Hit and Run Candlesticks will stay on top of the market pattern.
Free Trade Idea – KEM
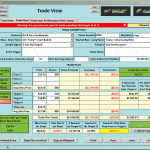 KEM (Kemet Corp) Continues to trend with several bullish chart patterns working. With Bullish follow through we will be looking for a couple of swings from 10% to 30%. We will share more about the KEM chart pattern in Trading Room #2 today.
KEM (Kemet Corp) Continues to trend with several bullish chart patterns working. With Bullish follow through we will be looking for a couple of swings from 10% to 30%. We will share more about the KEM chart pattern in Trading Room #2 today.
With on-demand recorded webinars, eBooks, and videos, member and non-member eLearning, plus the Live Trading Rooms, there is no end your education. Start small and learn
Conditions For The KEM Trade
- Doji Continuation pattern
- Cup & Handle
- Bullish J-Hook
- Rising
- Bullish Engulf (3-day chart)
- Doji Continuation
- Over 30% possible
Why Trade With Hit and Run Candlesticks
IRBT is up 19.18% from our members only post on May 2, 2017; Education builds confidence.
100 shares of IRBT was worth $1597.00 Yesterday – Subscribe Now
What is a Trade Idea Watchlist?
A trade idea watchlist is a list of stocks that we feel will move in our desired direction over a swing trader’s time frame. That time could be one to 15 days for example. From that watchlist, we wait until price action meets our conditions for a trade.
MEMBERS ONLY
Investing and Trading involve significant financial risk and are not suitable for everyone. No communication from Hit and Run Candlesticks Inc. is financial or trading advice. All information is intended for Educational Purposes Only. Terms of Service.
Rick Saddler is not a licensed financial adviser nor does he offer trade recommendations or advice to anyone except for the trading desk of Hit and Run Candlesticks Inc.
 KO | Options Trade of the Week | Video Reply
KO | Options Trade of the Week | Video Reply
-
- Trade Alert issued on April 26, 2017.
- Trade Closed June 2nd,2017.
- Trending stock traded with a Bull Call Debit Spread.
- The trade was closed for a 107% gain.
30-Day Trial | Hit & Run Candlesticks or Right Way Options
Investing and Trading involves significant financial risk and is not suitable for everyone. No communication from Hit and Run Candlesticks or it’s associates should be considered as financial or trading advice. All information is intended for Educational Purposes Only. Terms of Service
Productive price action as the market rests.
 Thus far the pullback/rest is showing productive price action in my opinion. Healthy markets commonly rest or pullback to test price supports. As of now, this resting pullback is not showing signs that the bears are taking over so far. Of course, that can always occur very quickly around new market highs. As the overall trend is still up will remain bullish, but I also want to be prepared in the event the Bears decide its time to feed. Always keep in mind that whipsaw price and swift reversal are common around potential market tops. Although fear is essentially not present at the moment we all know how quickly that can change so be prepared.
Thus far the pullback/rest is showing productive price action in my opinion. Healthy markets commonly rest or pullback to test price supports. As of now, this resting pullback is not showing signs that the bears are taking over so far. Of course, that can always occur very quickly around new market highs. As the overall trend is still up will remain bullish, but I also want to be prepared in the event the Bears decide its time to feed. Always keep in mind that whipsaw price and swift reversal are common around potential market tops. Although fear is essentially not present at the moment we all know how quickly that can change so be prepared.
On the Calendar
The only thing of significance on the Economic Calander this hump day is the EIA Petroleum Status Report at 10:30 AM Eastern. The last three reports have shown a decline in supplies, but the news lately from US producers suggest they have no intentions of slowing down. As a result oil prices and oil companies have continued to show weakness. Today’s number could easily move if this market.
On the Earnings Calendar, there are 29 companies expected to report earnings this morning. A quick scan of those on the docket there is none that would normally move the market. However, if you own or happen to be considering one of these companies, please understand the implications.
Action Plan
The market having rested a couple of days and pulling back to an area of possible support is healthy price action in my opinion. Futures have been dancing around the area of a flat open this morning. I think the Oil status number could be very influential on the market direction today. A build in supplies would be negative while a reduction in supply is positive for oil prices.
I will, of course, attend to current positions first but will continue looking for new long positions staying with the direction of the overall market. I will be very watchful for whipsaw price action at these levels and will exercise caution on new trades until I see the Bulls picking up their activity.
[button_2 color=”green” align=”center” href=”https://youtu.be/GGb-PcalicE”]Morning Market Prep Video[/button_2]
Trade Wisely,
Doug
SPY Performed Perfectly With A Bull Flag Breakout
(SPY) Last week the SPY performed perfectly with a bull flag breakout of the T-Line, A T-Line Run, A Flag PBO on support, then a Bull Kicker (was not perfect). The result is from the may 18, low to Friday’s June 2, close the Spay has run 3.13% (Sweet). While the market is bullish, we all should be doing very well in the charts we are trading. Keep your charts simple and clean so that you can see price. If you find yourself having trouble, reach out to one of our coaches.
FREE TRADE IDEA – JUNO
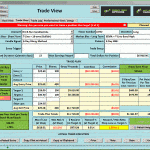 JUNO (Juno Therapeutics) has been rising for the past seven months; It is now above the 200-SMA on the daily chart. On the 3-day chart, JUNO is an RBB-pattern and has formed a Bullish Rising Method. Juno has also broken out of a downtrend line
JUNO (Juno Therapeutics) has been rising for the past seven months; It is now above the 200-SMA on the daily chart. On the 3-day chart, JUNO is an RBB-pattern and has formed a Bullish Rising Method. Juno has also broken out of a downtrend line
With on-demand recorded webinars, eBooks, and videos, member and non-member eLearning, plus the Live Trading Rooms, there is no end your education. Start small and learn
Conditions for the JUNO trade
- RBB (3-day chart)
- Rising
- Above resistance
- Morning Star (2-day chart)
- Rising Method (3-day chart)
- Over 25% possible
[button_1 text=”FREE%20J-Hook%20eBook%20-%20Great%20for%20Swing%20Traders” text_size=”32″ text_color=”#000000″ text_bold=”Y” text_letter_spacing=”0″ subtext_panel=”Y” subtext=”Click%20Here%20To%20Start%20Your%20Download” subtext_size=”15″ subtext_color=”#f50f0f” subtext_bold=”Y” subtext_letter_spacing=”0″ text_shadow_panel=”N” styling_width=”40″ styling_height=”30″ styling_border_color=”#000000″ styling_border_size=”1″ styling_border_radius=”6″ styling_border_opacity=”100″ styling_shine=”Y” styling_gradient_start_color=”#ffff00″ styling_gradient_end_color=”#ffa035″ drop_shadow_panel=”N” inset_shadow_panel=”N” align=”center” href=”https://hitandruncandlesticks.com/swing-traders-j-hook-pattern/” new_window=”Y”/]
Why Trade With Hit and Run Candlesticks
TDOCis up 50.57% from our members only post on February 28, 2017; Education builds confidence.
100 shares of SPWH was worth $2210.00 Friday –
What is a Trade Idea Watch List?
A trade idea watch list is a list of stocks that we feel will move in our desired direction over a swing trader’s time frame. That time could be one to 15 days for example. From that watch-list, we wait until price action meets our conditions for a trade.
Investing and Trading involve significant financial risk and is not suitable for everyone. No communication from Hit and Run Candlesticks Inc. is not financial or trading advice. All information is intended for Educational Purposes Only. Terms of Service.
Rick Saddler is not a licensed financial adviser nor does he offer trade recommendations or advise to anyone except for the trading desk of Hit and Run Candlesticks Inc.
 As I looked through the charts last night, I saw a lot of shooting stars and Doji’s at highs which are considered bearish. I also saw a lot of indecisive doji’s at highs and in consolidations. Both of these conditions would warrant significant caution. However, there was also a lot of very bullish patterns and some fantastic looking charts. What’s a guy to do? Yesterday was a very emotional day for the market due to the congressional hearings. There were several full reversal whipsaws during the day making charts very convoluted. As of now I’m staying bullish on the overall market and may even consider adding some risk ahead of the weekend, but I will give the market a good 30 minutes to an hour to settle in before making any decisions.
As I looked through the charts last night, I saw a lot of shooting stars and Doji’s at highs which are considered bearish. I also saw a lot of indecisive doji’s at highs and in consolidations. Both of these conditions would warrant significant caution. However, there was also a lot of very bullish patterns and some fantastic looking charts. What’s a guy to do? Yesterday was a very emotional day for the market due to the congressional hearings. There were several full reversal whipsaws during the day making charts very convoluted. As of now I’m staying bullish on the overall market and may even consider adding some risk ahead of the weekend, but I will give the market a good 30 minutes to an hour to settle in before making any decisions.






